Series Resistance
Ohm's Law teaches us that Voltage is equal to the product of resistance and
current. This is fine if we have a circuit as simple as a single light run by
a battery. But how often do we truly encounter a circuit which has only one
resistance? It is actually quite seldom. Most circuits have many resistances
in various combinations. So we must learn how to mathematically deal with all
these resistances. Fortunately, combined resistances can only be configured
in two ways:
Resistances Combined in Series
Resistances Combined in Parallel
We will discuss each of these separately. This class is dedicated to the study
of Resistances in Series, which you will find, are as simple as 2+2.
First, let us describe the difference between a SERIES circuit and a PARALLEL
circuit. A SERIES circuit is hooked together like a chain, with each link
connected to the link before it. If any given link in the chain is broken,
the whole chain is broken, and doesn't work.
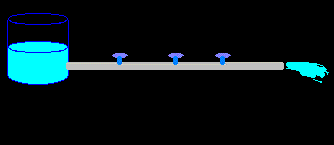 If we think of our circuit as a water pipe, a resistor could be a valve in the
pipe. A series circuit would have several valves in the same pipe. If we
shut the water off at any one valve, the water flow through the entire pipe
would be restricted. Let's say this again another way. The flow, or
current, is restricted by all the valves, but the valve with the most
resistance is the one that decreases the flow the most.
If we think of our circuit as a water pipe, a resistor could be a valve in the
pipe. A series circuit would have several valves in the same pipe. If we
shut the water off at any one valve, the water flow through the entire pipe
would be restricted. Let's say this again another way. The flow, or
current, is restricted by all the valves, but the valve with the most
resistance is the one that decreases the flow the most.
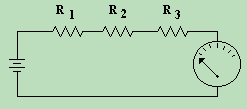 Now if we draw a schematic of resistors in series, it would look like the
diagram at the left. This first diagram would be an exact representation of
our waterflow circuit. The tank provides a source of water, just as a
battery supplies a source of electricity. The valves, which restrict the
flow of water, represent the resistors, which restrict the flow of electric
current.
Now if we draw a schematic of resistors in series, it would look like the
diagram at the left. This first diagram would be an exact representation of
our waterflow circuit. The tank provides a source of water, just as a
battery supplies a source of electricity. The valves, which restrict the
flow of water, represent the resistors, which restrict the flow of electric
current.
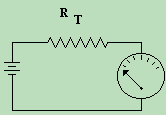 The diagram on the right shows the equivalent circuit, with only one resistor
(Rt) taking the place of all 3 resistors in the left diagram. Recall that
using an electrical equivalent circuit, that ANY circuit, no matter how
complex, can be represented with a single voltage source, and a single load.
The question is, how do we determine the value of the TOTAL resistance when
we have multiple resistors? This is the scope of this lesson. How do we
mathematically combine resistances that are connected in series?
The diagram on the right shows the equivalent circuit, with only one resistor
(Rt) taking the place of all 3 resistors in the left diagram. Recall that
using an electrical equivalent circuit, that ANY circuit, no matter how
complex, can be represented with a single voltage source, and a single load.
The question is, how do we determine the value of the TOTAL resistance when
we have multiple resistors? This is the scope of this lesson. How do we
mathematically combine resistances that are connected in series?
As I said before... it is as easy as 2+2. If two or more resistors are
connected end to end, as in a chain, we say that they are in series. To find
out the TOTAL RESISTANCE of resistors in series, all we have to do is add up
their individual values. It is that simple. If we have 3 resistors, (R1,
R2, and R3) each with a value of 2 Ω, the total resistance (RT) of
the series circuit would be 2+2+2, or a total of 6 Ω. Hence,
RT=R1+R2+R3+...
is the formula for resistors combined in series.
|



