Principles of Electricity



Resonance / Black Magic 101.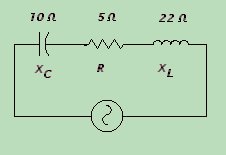

    In this circuit, we have a resistor, a capacitor, and a coil in series. Because the coil and the capacitor act in an opposite manner, they tend to cancel each other out. We say that the coil is additive, and the cap is subtractive in nature. If the inductive reactance, and the capacitive reactance were equal in value, they would effectively cancel each other completely out, and only the resistance would be seen. In this special case, we would say that we have a resonant circuit (we'll explain the term in more detail in a little bit).


Just as we must solve problems with resistance in series... we must also be able to add the various reactances together, and come up with a common ground. Resistance is pure resistance. Capacitive reactance is a resistance that is subtractive in nature. Inductive reactance is additive in nature. Combining the three, we come up with a new term called IMPEDANCE, which is symbolized by the letter Z. Just like resistance, the formula is different for impedance in series and in parallel. The formula for impedance in series is: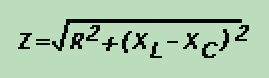
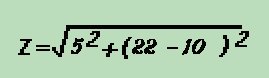
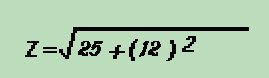
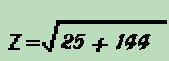
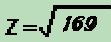
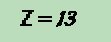If we plug in the values in the example above, we can solve the formula like so:







Note that this method is not much different than what we did in lesson 25. There we added phase "vectorally". This is a function of trigenometry, where in a given triangle, A2+B2=C2. (The square of the hypotenuse is equal to the sum of the square of the two sides). The same applies here.

We can say that the A2 is the resistance, the B2 is the combined capacitive and inductive reactances, and the C2 is the Impedance ( Z ).

We could plot out our capacitance and inductance vectorally, but this would use up lots of time and paper. We can simply solve the same problem using this formula, where the B2 is equal to the sum of the reactances of the coil and the cap. We always subtract the capacitive reactance from the inductive reactance, because capacitors are subtractive.

So if I hate math so much, why do I say that this is where the real fun begins? You'll see!
(On The Following Indicator... PURPLE will indicate your current location)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75

[COURSE INDEX] [ELECTRONICS GLOSSARY] [HOME]

Otherwise - please click to visit an advertiser so they know you saw their ad!


This Course was written by Ray Dall © All Rights Reserved.
This page and all its content Copyright, Trademarks, Intellectual Properties
and other legal issues 1994, 1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011 Ray Dall.
All Rights Reserved.
And for what it's worth... this page was last updated HexDate 01-11--7D1

VISITORS:
Add Me!