


RL and RC Time Constants.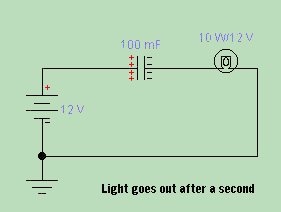
In this circuit, the moment the battery is applied, current starts to flow through the resistor, and a voltage begins to build up across the plates of the capacitor. The amount of time that it takes for the voltage across the capacitor plates to reach the voltage of the battery, is a result of the values of the capacitor and the resistor. The larger these two values are, the longer it will take for the entire voltage to appear across the cap. This relationship is expressed by a formula, and is called "Time Constant". The formula is: where T= Time in seconds, R=resistance in ohms, and C=capacitance in farads. A time constant also exists between coils and resistors, however, because of the nature of how a coil is made (it is essentially a piece of wire), time constants in RL circuits are much smaller. Recall that earlier in the course, we discussed that inductors and capacitors are almost exact opposites. Here is another formula which will seem re-hashed. where T= Time in seconds, R=resistance in ohms, and L=inductance in henries. Remember this formula? Well, you are going to have to start using XL and XC again. Because we are going to begin using capacitors and coils in the same circuit. Now the real fun of electronics begins. |
| (On The Following Indicator... PURPLE will indicate your current location) | ||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| Otherwise - please click to visit an advertiser so they know you saw their ad! |
