


Series - Parallel Resistances the Combination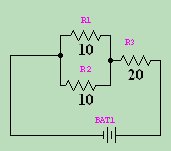 If you look at the example on the right, it has 3 resistors and 1 battery. R
1
and R
2
are both 10 Ω in parallel.
If you look at the example on the right, it has 3 resistors and 1 battery. R
1
and R
2
are both 10 Ω in parallel.
------------ 1 1 ---- + ---- R 1 R 2 We can say that: 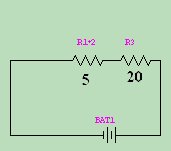 We also have R
3
in the circuit, which is 20Ω. Once we have combined the 2 parallel
resistors, we have a simpler circuit.... 2 series resistors. R
1&2
and R
3
. If we add the value of these two resistors, we come up with
We also have R
3
in the circuit, which is 20Ω. Once we have combined the 2 parallel
resistors, we have a simpler circuit.... 2 series resistors. R
1&2
and R
3
. If we add the value of these two resistors, we come up with
Then if we know the voltage, we can find the current through the entire circuit, and through each individual resistor. Go ahead and try plugging in a voltage (like 25V) and finding the currents. You'll be surprised at how simple it is. 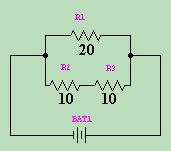 Let's try another example. In the circuit on the right, we have 3 resistors
again. But this time, they are configured differently. Do you see how you
would combine them for the total resistance? First, you must add the 10
Ω resistors by adding them. This is simple because they are in Series.
Let's try another example. In the circuit on the right, we have 3 resistors
again. But this time, they are configured differently. Do you see how you
would combine them for the total resistance? First, you must add the 10
Ω resistors by adding them. This is simple because they are in Series.
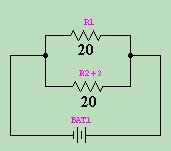 Using our parallel circuit formula then:
Using our parallel circuit formula then:
------------ 1 1 ---- + ---- R 1 R 2 |
[COURSE INDEX] [ELECTRONICS GLOSSARY] [HOME]
| Otherwise - please click to visit an advertiser so they know you saw their ad! |
